Publications
Highlights
(For a full list of publications and patents see below or go to Google Scholar.
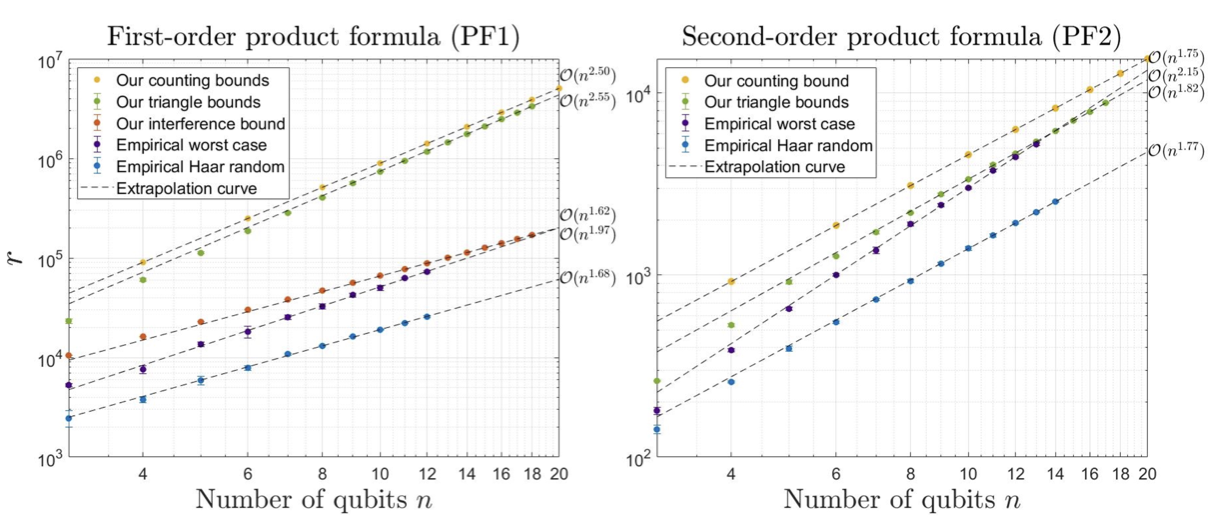
The algorithmic error of digital quantum simulations is usually explored in terms of the spectral norm distance between the actual and ideal evolution operators. In practice, this worst-case error analysis may be unnecessarily pessimistic. To address this, we develop a theory of average-case performance of Hamiltonian simulation with random initial states. We relate the average-case error to the Frobenius norm of the multiplicative error and give upper bounds for the product formula (PF) and truncated Taylor series methods. As applications, we estimate average-case error for the digital Hamiltonian simulation of general lattice Hamiltonians and k-local Hamiltonians. In particular, for the nearest-neighbor Heisenberg chain with n spins, the error is quadratically reduced from O(n) in the worst case to O(√n) on average for both the PF method and the Taylor series method. Numerical evidence suggests that this theory accurately characterizes the average error for concrete models. We also apply our results to error analysis in the simulation of quantum scrambling.
Q. Zhao, Y. Zhou, A. F. Shaw, T. Li, and A. M. Childs.
Phys. Rev. Lett., vol. 129, p. 270502 , QIP 2022 contributed talk
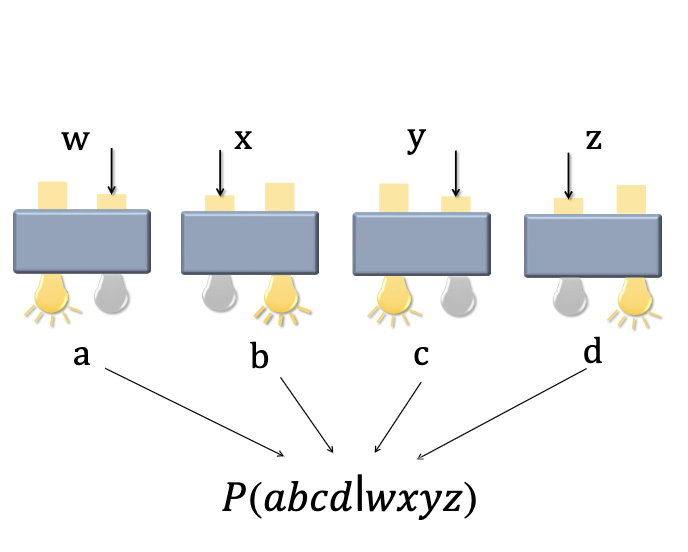
Here, we demonstrate the first robust self-testing for multi-particle quantum entanglement. We prepare two examples of four-photon graph states, the Greenberger-Horne-Zeilinger (GHZ) states with a fidelity of 0.957(2) and the linear cluster states with a fidelity of 0.945(2). Based on the observed input-output statistics, we certify the genuine four-photon entanglement and further estimate their qualities with respect to realistic noise in a device-independent manner.
D. Wu, Q. Zhao (Co-first author), X.-M. Gu, H.-S. Zhong, Y. Zhou, L.-C. Peng, J. Qin, Y.-H. Luo,K. Chen, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W.
Phys. Rev. Lett., vol. 127, p. 230503, Dec. 2021
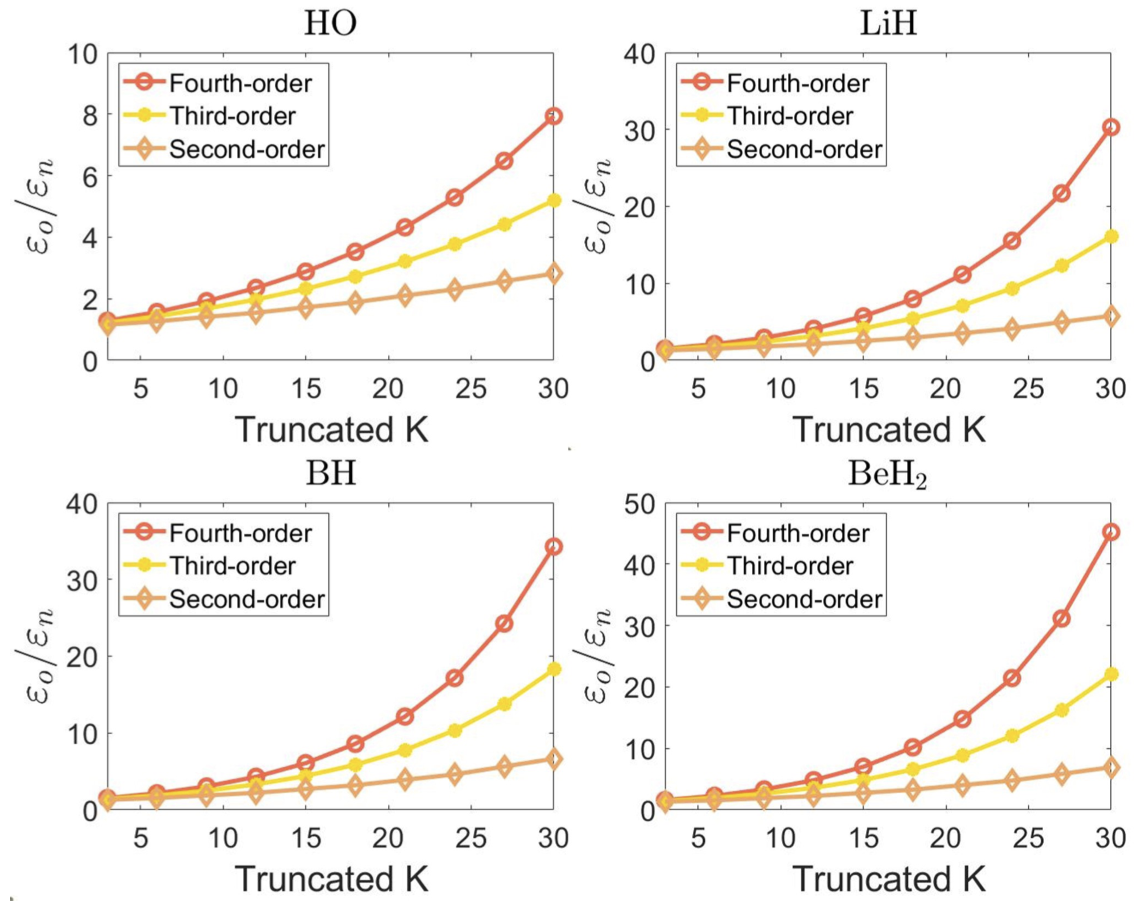
Here, we theoretically explore the role of anti-commutative relation in Hamiltonian simulation. We find that, contrary to our intuition, anticommutative relations could also reduce the hardness of Hamiltonian simulation. Specifically, Hamiltonians with mutually anti-commutative terms are easy to simulate, as what happens with ones consisting of mutually commutative terms. Such a property is further utilized to reduce the algorithmic error or the gate complexity in the truncated Taylor series quantum algorithm for general problems. Moreover, we propose two modified linear combinations of unitaries methods tailored for Hamiltonians with different degrees of anti-commutation. We numerically verify that the proposed methods exploiting anti-commutative relations could significantly improve the simulation accuracy of electronic Hamiltonians.
Q. Zhao and X. Yuan
Quantum, vol. 5, p.534, Aug. 2021
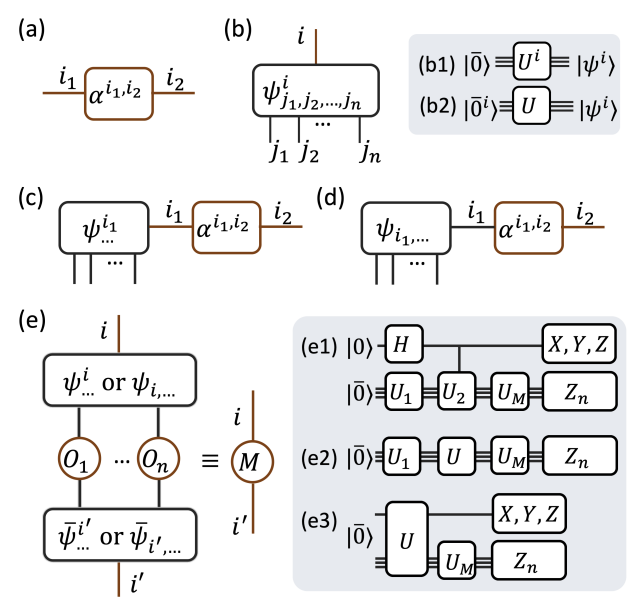
Here, we introduce the framework of hybrid tensor networks with building blocks consisting of measurable quantum states and classically contractable tensors, inheriting both their distinct features in efficient representation of many-body wave functions. With the example of hybrid tree tensor networks, we demonstrate efficient quantum simulation using a quantum computer whose size is significantly smaller than the one of the target system.
X. Yuan, J. Sun, J. Liu, Q. Zhao, and Y. Zhou
Phys. Rev. Lett., vol. 127, p. 040501, Jul 2021.

Here, for the first time, we demonstrate MDIEW for multipartite entangled states. We experimentally detect the genuine entanglement and the entanglement structure of a tripartite entangled state based on an eight-photon interferometry. Furthermore, with the verified multipartite entangled state, we demonstrate quantum randomness generation and open-destination quantum key distribution in an measurement-device-independent manner.
Z.-D. Li, Q. Zhao (Co-first author), R. Zhang, L.-Z. Liu, X.-F. Yin, X. Zhang, Y.-Y. Fei, K. Chen, N.-L. Liu, F. Xu, Y.-A. Chen, L. Li, and J.-W. Pan
Phys. Rev. Lett., vol. 124, p. 160503, Apr 2020.
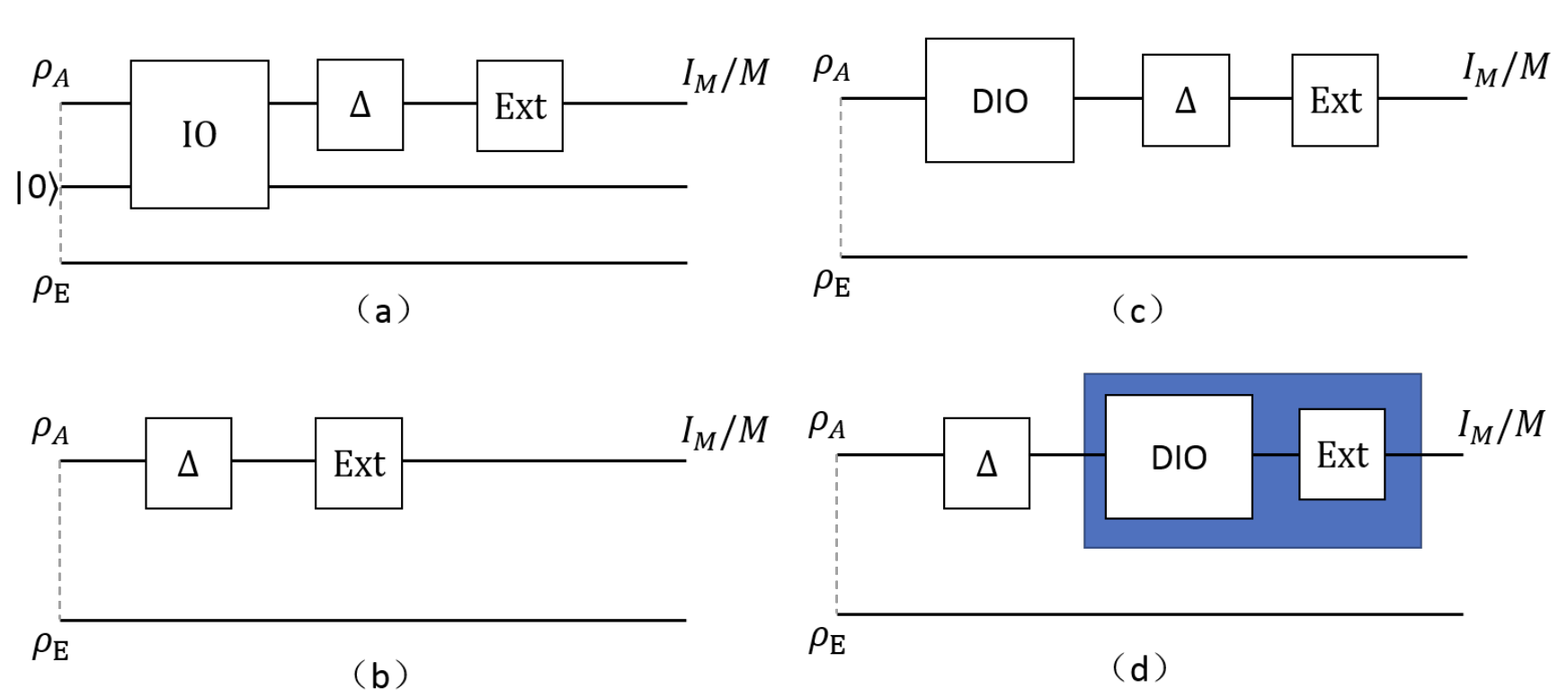
We consider the one-shot problem of distilling pure coherence from a single instance of a given resource state. Specifically, we determine the distillable coherence with a given fidelity under incoherent operations (IO) through a generalization of the Winter-Yang protocol. We also relate the distillable coherence under strictly incoherent operations (SIO) to a constrained hypothesis testing.
Q. Zhao*, Y. Liu, X. Yuan, E. Chitambar, and A.Winter
IEEE Transactions on Information Theory, vol. 65, no. 10, pp. 6441–6453, 2019.
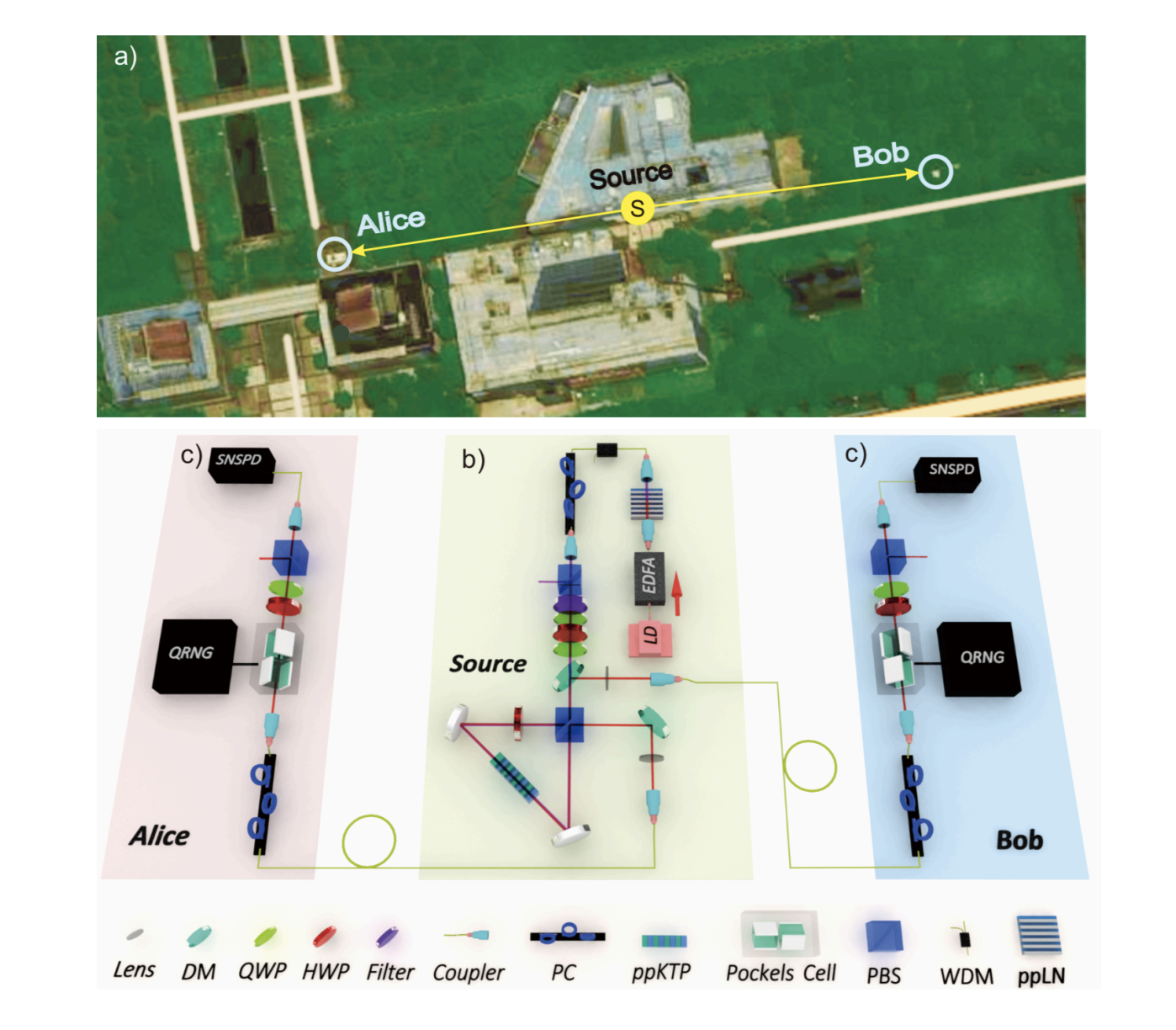
Here we present DIQRNG that is secure against quantum and classical adversaries10–12. We use state-of-the-art quantum optical technology to create, modulate and detect entangled photon pairs, achieving an efficiency of more than 78 per cent from creation to detection at a distance of about 200 metres that greatly exceeds the threshold for closing the ‘detection’ loophole of the Bell test.
Y. Liu, Q. Zhao, M.-H. Li, J.-Y. Guan, Y. Zhang, B. Bai,W. Zhang,W.-Z. Liu, C.Wu, X. Yuan, H. Li, W. J. Munro, Z.Wang, L. You, J. Zhang, X. Ma, J. Fan, Q. Zhang, and J.-W. Pan
Nature, vol. 562, no. 7728, p. 548, 2018.
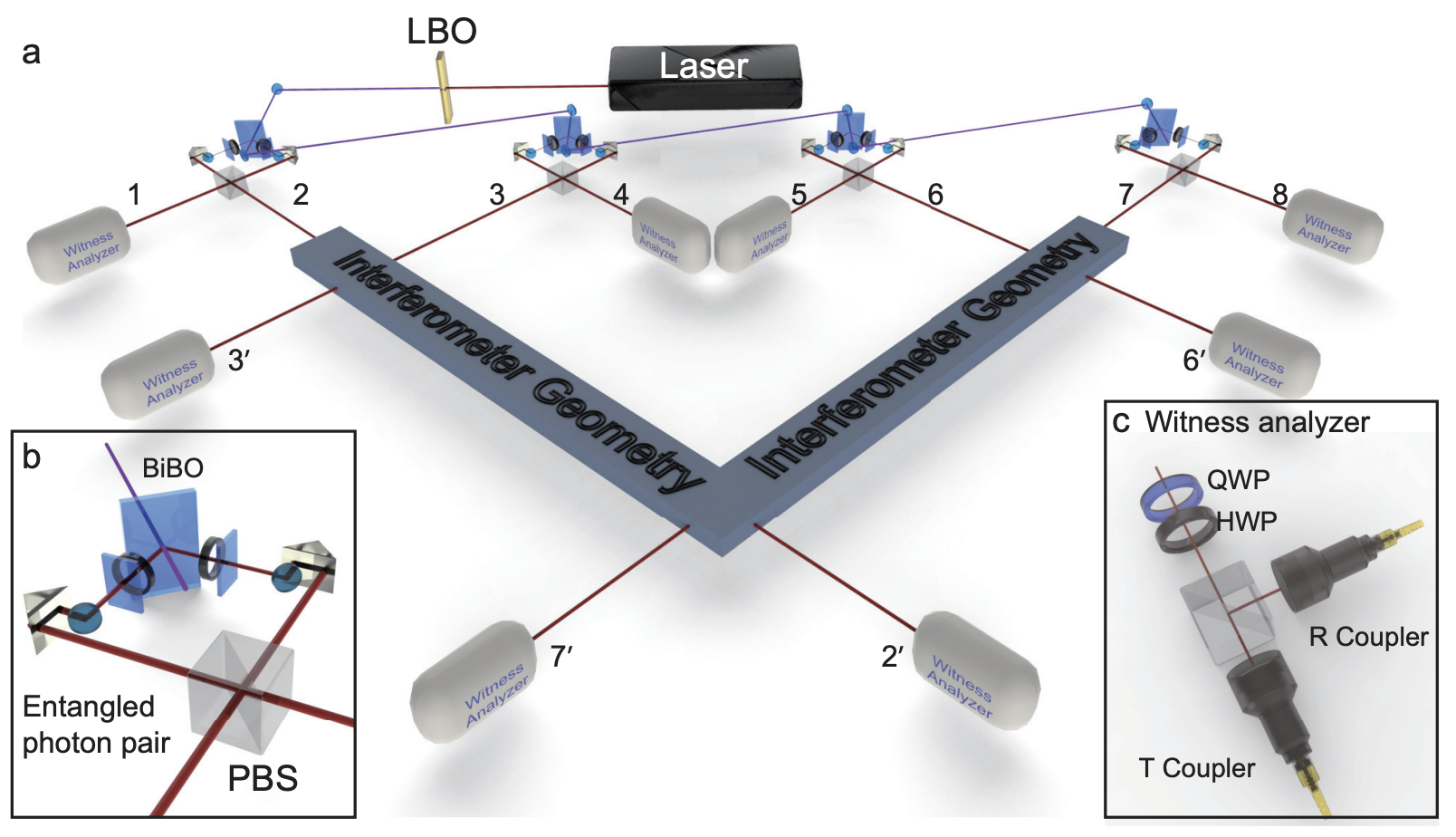
Here, we propose two complementary families of witnesses for the identification of such structures. They are based, respectively, on the detection of entanglement intactness and entanglement depth, each applicable to an arbitrary number of subsystems and whose evaluation requires only the implementation of solely two local measurements. Our method is also robust against noises and other imperfections, as reflected by our experimental implementation of these tools to verify the entanglement structure of five different eight-photon entangled states. In particular, we demonstrate how their entanglement structure can be precisely and systematically inferred from the experimental measurement of these witnesses. In achieving this goal, we also illustrate how the same set of data can be classically postprocessed to learn the most about the measured system.
H. Lu, Q. Zhao (Co-first author), Z.-D. Li, X.-F. Yin, X. Yuan, J.-C. Hung, L.-K. Chen, L. Li, N.-L. Liu, C.-Z. Peng, Y.-C. Liang, X. Ma, Y.-A. Chen, and J.-W. Pan
Phys. Rev. X, vol. 8, p. 021072, Jun 2018.
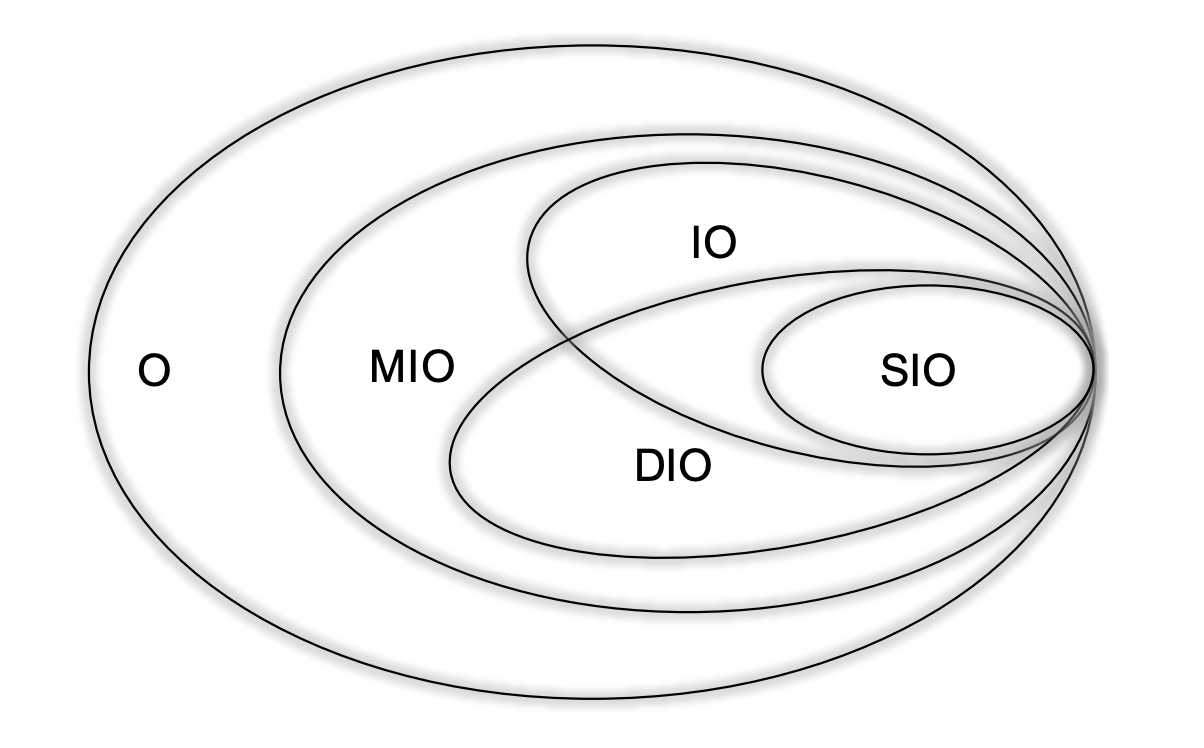
This Letter establishes the one-shot theory of coherence dilution, which involves converting maximally coherent states into an arbitrary quantum state using maximally incoherent operations, dephasing-covariant incoherent operations, incoherent operations, or strictly incoherent operations. We introduce several coherence monotones with concrete operational interpretations that estimate the one-shot coherence cost—the minimum amount of maximally coherent states needed for faithful coherence dilution. Furthermore, we derive the asymptotic coherence dilution results with maximally incoherent operations, incoherent operations, and strictly incoherent operations as special cases. Our result can be applied in the analyses of quantum information processing tasks that exploit coherence as resources, such as quantum key distribution and random number generation.
Q. Zhao, Y. Liu, X. Yuan, E. Chitambar, and X. Ma
Phys. Rev. Lett., vol. 120, p. 070403, Feb 2018.
To date, blind quantum computing demonstrations require clients to have weak quantum devices. Here we implement a proof-of-principle experiment for completely classical clients. Via classically interacting with two quantum servers that share entanglement, the client accomplishes the task of having the number 15 factorized by servers who are denied information about the computation itself. This concealment is accompanied by a verification protocol that tests servers’ honesty and correctness. Our demonstration shows the feasibility of completely classical clients and thus is a key milestone towards secure cloud quantum computing.
H.-L. Huang, Q. Zhao, X. Ma, C. Liu, Z.-E. Su, X.-L.Wang, L. Li, N.-L. Liu, B. C. Sanders, C.-Y. Lu, and J.-W. Pan
Phys. Rev. Lett., vol. 119, p.050503, Aug 2017.
Full List of Publications
-
Graph-theoretic characterization of unextendible product bases
Fei Shi, Ge Bai, Xiande Zhang, Qi Zhao, and Giulio Chiribella
Phys. Rev. Research 5, 033144 -
A theory of quantum differential equation solvers: limitations and fast-forwarding
Dong An, Jin-Peng Liu, Daochen Wang, Qi Zhao.
arXiv:2211.05246 -
Unextendible and uncompletable product bases in every bipartition
Fei Shi, Mao-Sheng Li, Xiande Zhang, Qi Zhao.
New J. Phys. 24 113025 -
Efficient and practical quantum compiler towards multi-qubit systems with deep reinforcement learning
Qiuhao Chen, Yuxuan Du, Qi Zhao, Yuling Jiao, Xiliang Lu, Xingyao Wu.
arXiv:2204.06904 -
Closing the Locality and Detection Loopholes in Multiparticle Entanglement Self-Testing
Dian Wu, Qi Zhao (Co-first author), Can Wang, Liang Huang, Yang-Fan Jiang, Bing Bai, You Zhou, Xue-Mei Gu, Feng-Ming Liu, Ying-Qiu Mao, Qi-Chao Sun, Ming-Cheng Chen, Jun Zhang, Cheng-Zhi Peng, Xiao-Bo Zhu, Qiang Zhang, Chao-Yang Lu, and Jian-Wei Pan.
Physical Review Letters 128 (25), 250401 -
Computational self-testing of multi-qubit states and measurements
H. Fu, D. Wang, and Q. Zhao.
ArXiv 2201.13430 -
Hamiltonian simulation with random inputs
Q. Zhao, Y. Zhou, A. F. Shaw, T. Li, and A. M. Childs.
Phys. Rev. Lett., vol. 129, p. 270502 , QIP 2022 contributed talk -
Robust self-testing of multiparticle entanglement
D. Wu, Q. Zhao (Co-first author), X.-M. Gu, H.-S. Zhong, Y. Zhou, L.-C. Peng, J. Qin, Y.-H. Luo,K. Chen, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W.
Phys. Rev. Lett., vol. 127, p. 230503, Dec. 2021 -
Exploiting anticommutation in Hamiltonian simulation
Q. Zhao and X. Yuan
Quantum, vol. 5, p.534, Aug. 2021 -
Quantum teleportation of physical qubits into logical code spaces
Y.-H. Luo, M.-C. Chen, M. Erhard, H.-S. Zhong, D. Wu, H.-Y. Tang, Q. Zhao, X.-L. Wang, K. Fujii, L. Li, N.-L. Liu, K. Nemoto, W. J. Munro, C.-Y. Lu, A. Zeilinger, and J.-W. Pan,
Proceedings of the National Academy of Sciences, vol. 118, no. 36, 2021. -
Quantum simulation with hybrid tensor networks
X. Yuan, J. Sun, J. Liu, Q. Zhao, and Y. Zhou
Phys. Rev. Lett., vol. 127, p. 040501, Jul 2021. -
Universal and operational benchmarking of quantum memories
X. Yuan, Y. Liu, Q. Zhao, B. Regula, J. Thompson, and M. Gu
npj Quantum Information, vol. 7, no. 1, pp. 1–8, 2021. -
Entanglement-free witnessing of quantum incompatibility in a high-dimensional system
D.Wu, Q. Zhao* (Co-first author), Y.-H. Luo, H.-S. Zhong, L.-C. Peng, K. Chen, P. Xue, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W. Pan
Phys. Rev. Research, vol. 3, p. 023017, Apr 2021. -
Experimental realization of device-independent quantum randomness expansion
M.-H. Li, X. Zhang,W.-Z. Liu, S.-R. Zhao, B. Bai, Y. Liu, Q. Zhao, Y. Peng, J. Zhang, Y. Zhang, W. J. Munro, X. Ma, Q. Zhang, J. Fan, and J.-W. Pan
Phys. Rev. Lett., vol. 126, p. 050503, Feb 2021. -
Experimental exploration of five-qubit quantum error correcting code with superconducting qubits
M. Gong, X. Yuan, S.Wang, Y. Wu, Y. Zhao, C. Zha, S. Li, Z. Zhang, Q. Zhao, Y. Liu, F. Liang, J. Lin, Y. Xu, H. Deng, H. Rong, H. Lu, S. C. Benjamin, C.-Z. Peng, X. Ma, Y.-A. Chen, X. Zhu, and J.-W. Pan
National Science Review, 01 2021, nwab011. -
Measurement-device-independent entanglement witness of tripartite entangled states and its applications
Z.-D. Li, Q. Zhao (Co-first author), R. Zhang, L.-Z. Liu, X.-F. Yin, X. Zhang, Y.-Y. Fei, K. Chen, N.-L. Liu, F. Xu, Y.-A. Chen, L. Li, and J.-W. Pan
Phys. Rev. Lett., vol. 124, p. 160503, Apr 2020. -
Randomness expansion secured by quantum contextuality
M. Um, Q. Zhao (Co-first author), J. Zhang, P.Wang, Y.Wang, M. Qiao, H. Zhou, X. Ma, and K. Kim
Phys. Rev. Applied, vol. 13, p. 034077, Mar 2020. -
Simultaneous certification of entangled states and measurements in bounded dimensional semiquantum games
X. Zhang and Q. Zhao*
Phys. Rev. Research, vol. 2, p. 033400, Sep 2020. -
High-threshold code for modular hardware with asymmetric noise
X. Xu, Q. Zhao, X. Yuan, and S. C. Benjamin
Phys. Rev. Applied, vol. 12, p. 064006, Dec 2019. -
Theory of variational quantum simulation
X. Yuan, S. Endo, Q. Zhao, Y. Li, and S. C. Benjamin
Quantum, vol. 3, p. 191, Oct. 2019. [Online]. -
One-shot coherence distillation with catalysts
S. Chen, X. Zhang, Y. Zhou, and Q. Zhao*
Phys. Rev. A, vol. 100, p. 042323, Oct 2019. -
Detecting multipartite entanglement structure with minimal resources
Y. Zhou, Q. Zhao, X. Yuan, and X. Ma
npj Quantum Information, vol. 5, p. 83, 2019. -
Quantum coherence and intrinsic randomness
X. Yuan, Q. Zhao, D. Girolami, and X. Ma
Quantum Technologies, vol. 0, no. 0, p. 1900053. -
Efficient and robust detection of multipartite greenberger-horne-zeilinger-like states
Q. Zhao, G.Wang, X. Yuan, and X. Ma
Phys. Rev. A, vol. 99, p. 052349, May 2019. -
Compatibility of causal hidden-variable theories with a delayed-choice experiment
H.-L. Huang, Y.-H. Luo, B. Bai, Y.-H. Deng, H.Wang, Q. Zhao*, H.-S. Zhong, Y.-Q. Nie,W.-H. Jiang, X.-L.Wang, J. Zhang, L. Li, N.-L. Liu, T. Byrnes, J. P. Dowling, C.-Y. Lu, and J.-W. Pan
Phys. Rev. A, vol. 100, p. 012114, Jul 2019. -
One-shot coherence distillation: Towards completing the picture
Q. Zhao*, Y. Liu, X. Yuan, E. Chitambar, and A.Winter
IEEE Transactions on Information Theory, vol. 65, no. 10, pp. 6441–6453, 2019. -
Mitigating algorithmic errors in a hamiltonian simulation
S. Endo, Q. Zhao, Y. Li, S. Benjamin, and X. Yuan
Phys. Rev. A, vol. 99, p. 012334, Jan 2019. -
Device-independent quantum random-number generation
Y. Liu, Q. Zhao, M.-H. Li, J.-Y. Guan, Y. Zhang, B. Bai,W. Zhang,W.-Z. Liu, C.Wu, X. Yuan, H. Li, W. J. Munro, Z.Wang, L. You, J. Zhang, X. Ma, J. Fan, Q. Zhang, and J.-W. Pan
Nature, vol. 562, no. 7728, p. 548, 2018. -
Test of local realism into the past without detection and locality loopholes
M.-H. Li, C.Wu, Y. Zhang,W.-Z. Liu, B. Bai, Y. Liu,W. Zhang, Q. Zhao, H. Li, Z.Wang, L. You, W. J. Munro, J. Yin, J. Zhang, C.-Z. Peng, X. Ma, Q. Zhang, J. Fan, and J.-W. Pan
Phys. Rev. Lett., vol. 121, p. 080404, Aug 2018. -
Entanglement structure: Entanglement partitioning in multipartite systems and its experimental detection using optimizable witnesses
H. Lu, Q. Zhao (Co-first author), Z.-D. Li, X.-F. Yin, X. Yuan, J.-C. Hung, L.-K. Chen, L. Li, N.-L. Liu, C.-Z. Peng, Y.-C. Liang, X. Ma, Y.-A. Chen, and J.-W. Pan
Phys. Rev. X, vol. 8, p. 021072, Jun 2018. -
Quantum coherence via conditional entropy
Y. Liu, Q. Zhao (Co-first author), and X. Yuan
Journal of Physics A Mathematical and Theoretical, vol. 51, no. 41, p. 414018, 2018. -
One-shot coherence dilution
Q. Zhao, Y. Liu, X. Yuan, E. Chitambar, and X. Ma
Phys. Rev. Lett., vol. 120, p. 070403, Feb 2018. -
High-speed device-independent quantum random number generation without a detection loophole
Y. Liu, X. Yuan, M.-H. Li, W. Zhang, Q. Zhao, J. Zhong, Y. Cao, Y.-H. Li, L.-K. Chen, H. Li, T. Peng, Y.-A. Chen, C.-Z. Peng, S.-C. Shi, Z.Wang, L. You, X. Ma, J. Fan, Q. Zhang, and J.-W. Pan
Phys. Rev. Lett., vol. 120, p. 010503, Jan 2018. -
Polynomial measure of coherence
Y. Zhou, Q. Zhao*, X. Yuan, and X. Ma
New Journal of Physics, vol. 19, no. 12, p. 123033, 2017. -
Experimental blind quantum computing for a classical client
H.-L. Huang, Q. Zhao, X. Ma, C. Liu, Z.-E. Su, X.-L.Wang, L. Li, N.-L. Liu, B. C. Sanders, C.-Y. Lu, and J.-W. Pan
Phys. Rev. Lett., vol. 119, p.050503, Aug 2017. -
Experimental measurement-device-independent quantum digital signatures over a metropolitan network
H.-L. Yin,W.-L.Wang, Y.-L. Tang, Q. Zhao, H. Liu, X.-X. Sun,W.-J. Zhang, H. Li, I. V. Puthoor, L.-X. You, E. Andersson, Z. Wang, Y. Liu, X. Jiang, X. Ma, Q. Zhang, M. Curty, T.-Y. Chen, and J.-W. Pan
Phys. Rev. A, vol. 95, p. 042338, Apr 2017. -
Entanglement swapping with independent sources over an optical-fiber network
Q.-C. Sun, Y.-L. Mao, Y.-F. Jiang, Q. Zhao, S.-J. Chen,W. Zhang,W.-J. Zhang, X. Jiang, T.-Y. Chen, L.-X. You, L. Li, Y.-D. Huang, X.-F. Chen, Z.Wang, X. Ma, Q. Zhang, and J.-W. Pan
Phys. Rev. A, vol. 95, p. 032306, Mar 2017. -
Improved key-rate bounds for practical decoy-state quantum-key-distribution systems
Z. Zhang, Q. Zhao, M. Razavi, and X. Ma
Phys. Rev. A, vol. 95, p. 012333, Jan 2017. -
Efficient measurement-device-independent detection of multipartite entanglement structure
Q. Zhao, X. Yuan, and X. Ma
Phys. Rev. A, vol. 94, p. 012343, Jul 2016. -
Performance of device-independent quantum key distribution
Z. Cao, Q. Zhao, and X. Ma
Phys. Rev. A, vol. 94, p. 012319, Jul 2016. -
Measurement-device-independent quantum key distribution over untrustful metropolitan network
Y.-L. Tang, H.-L. Yin, Q. Zhao, H. Liu, X.-X. Sun, M.-Q. Huang,W.-J. Zhang, S.-J. Chen, L. Zhang, L.-X. You, Z.Wang, Y. Liu, C.-Y. Lu, X. Jiang, X. Ma, Q. Zhang, T.-Y. Chen, and J.-W. Pan
Phys. Rev. X, vol. 6, p. 011024, Mar 2016. -
Clauser-horne bell test with imperfect random inputs
X. Yuan, Q. Zhao, and X. Ma
Phys. Rev. A, vol. 92, p. 022107, Aug 2015. -
One-shot dynamical resource theory
X. Yuan, P. Zeng, M. Gao, and Q. Zhao
ArXiv:2012.02781, 2020. -
Constructing multipartite bell inequalities from stabilizers
Q. Zhao and Y. Zhou
ArXiv:2002.01843, 2020. -
Quantifying coherenceandentanglement via simple measurements
G. Smith, J. A. Smolin, X. Yuan, Q. Zhao, D. Girolami, and X. Ma,
ArXiv:1707.09928, 2017.
Patents
Xiongfeng Ma and Qi Zhao
Measurement-device-independent quantum key distribution with biasedbasis choice
Patent number: ZL201621455743.9
Xiongfeng Ma and Qi Zhao
Quantum key distribution based on two-way classical communication
Patent number: ZL201621440463.0
Xiongfeng Ma and Qi Zhao
Quantum key distribution data postprocessing for detector efficiencymismatc
Patent number: CN105049200A