Research Directions
Our research focuses on two main areas in the intersection of quantum physics and computer science. In Quantum Computing, we explore Quantum Simulation and Quantum Scientific Computing. In Quantum Information, we investigate Entanglement Detection and Device-Independent protocols. Representative highlights showcase our key contributions in each area.
Quantum Computing
Quantum Simulation
Q. Zhao, Y. Zhou, and A. M. Childs, Nature Physics, vol. 21, p. 1338–1345, 2025, QIP 2025 contributed talk

Quantum entanglement is an essential feature of many-body systems that impacts both quantum information processing and fundamental physics. Classical simulation methods can efficiently simulate many-body states with low entanglement, but struggle as the degree of entanglement grows. Here we investigate the relationship between quantum entanglement and quantum simulation, and show that product formula approximations for simulating many-body systems can perform better for entangled systems. We establish an upper bound for algorithmic error in terms of entanglement entropy that is tighter than previous results, and develop an adaptive simulation algorithm that incorporates measurement gadgets to estimate the algorithmic error. This shows that entanglement is not only an obstacle to classical simulation, but also a feature that can accelerate quantum algorithms.
Q. Zhao, Y. Zhou, A. F. Shaw, T. Li, and A. M. Childs, Phys. Rev. Lett., vol. 129, p. 270502 , QIP 2022 contributed talk
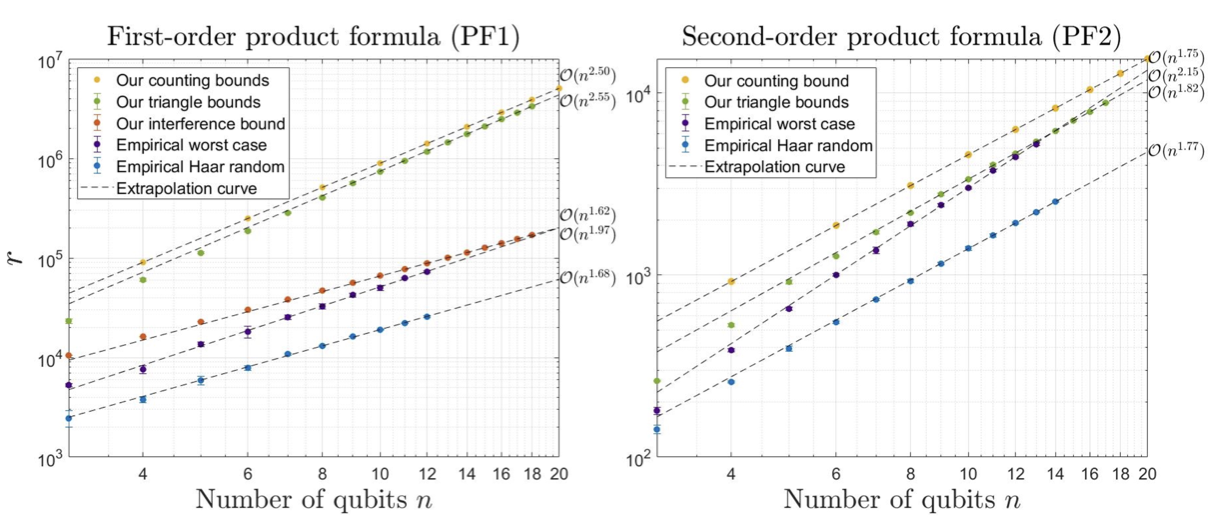
The algorithmic error of digital quantum simulations is usually explored in terms of the spectral norm distance between the actual and ideal evolution operators. In practice, this worst-case error analysis may be unnecessarily pessimistic. To address this, we develop a theory of average-case performance of Hamiltonian simulation with random initial states. We relate the average-case error to the Frobenius norm of the multiplicative error and give upper bounds for the product formula (PF) and truncated Taylor series methods. As applications, we estimate average-case error for the digital Hamiltonian simulation of general lattice Hamiltonians and k-local Hamiltonians. In particular, for the nearest-neighbor Heisenberg chain with n spins, the error is quadratically reduced from O(n) in the worst case to O(√n) on average for both the PF method and the Taylor series method. Numerical evidence suggests that this theory accurately characterizes the average error for concrete models. We also apply our results to error analysis in the simulation of quantum scrambling.
W. Yu, J. Xu, and Q. Zhao, Communications Physics, vol. 8, no. 1, p. 340, 2025.
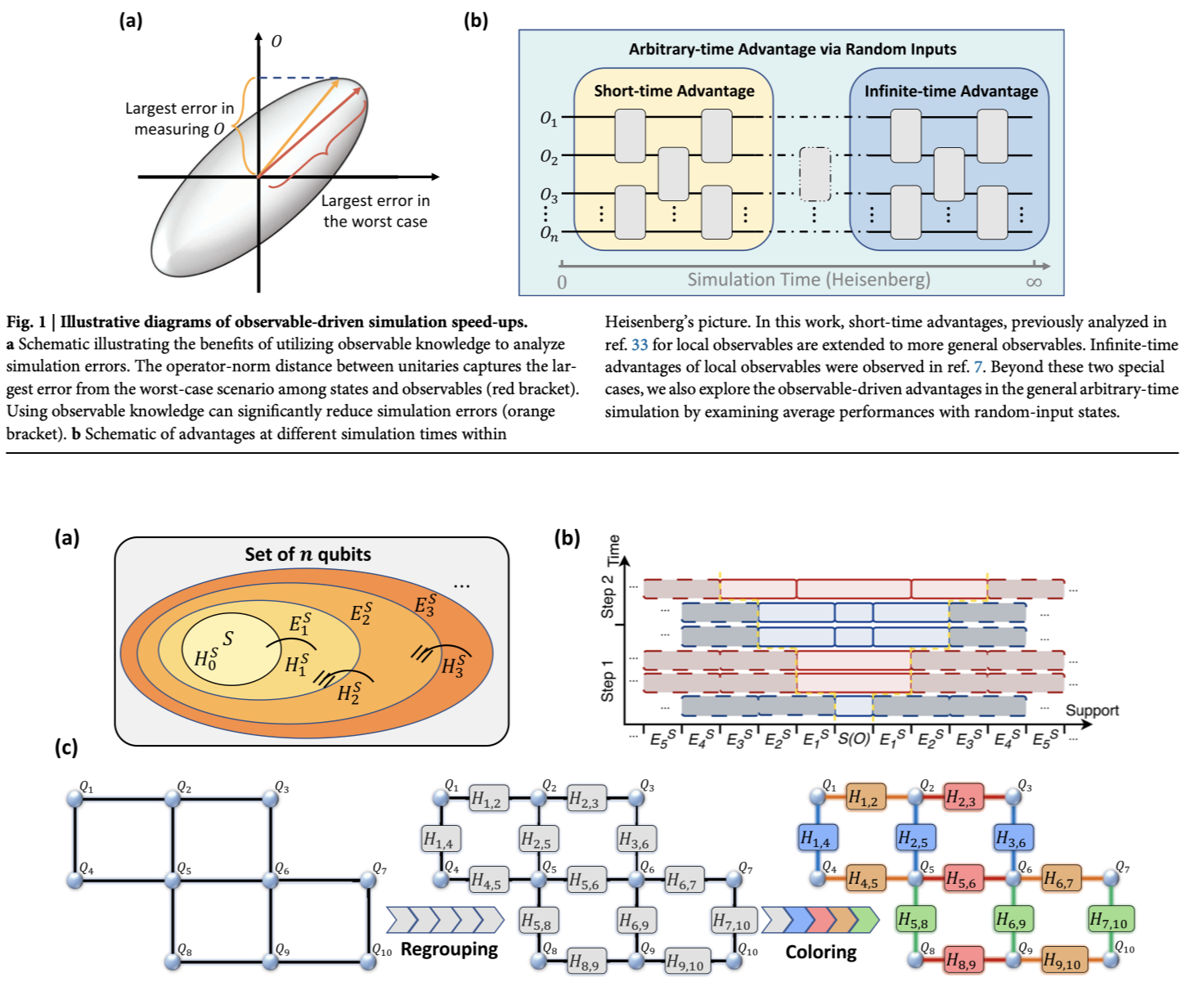
Quantum simulation represents a cornerstone application for quantum computers, offering the potential to solve classically intractable problems in physics, chemistry, and materials science. Despite being one of the most accessible simulation methods, the product formula encounters challenges due to the pessimistic gate count estimation. In this work, we elucidate how observable knowledge can accelerate quantum simulations. By focusing on specific knowledge of observables, we reduce product-formula simulation errors and gate counts in both short-time and arbitrary-time scenarios. For short-time simulations, we deliberately design and tailor product formulas to achieve size-independent errors for local and certain global observables. In arbitrary-time simulations, we reveal that Pauli-summation structured observables generally reduce average errors with a typically quadratic error reduction. Our advanced error analyses, supported by numerical studies, indicate improved gate count estimation. We anticipate that the explored speed-ups can pave the way for efficiently realizing quantum simulations and demonstrating advantages on near-term quantum devices.
P. Zeng, J. Sun, L. Jiang, and Q. Zhao, PRX Quantum, vol. 6, p. 010359, Mar 2025.
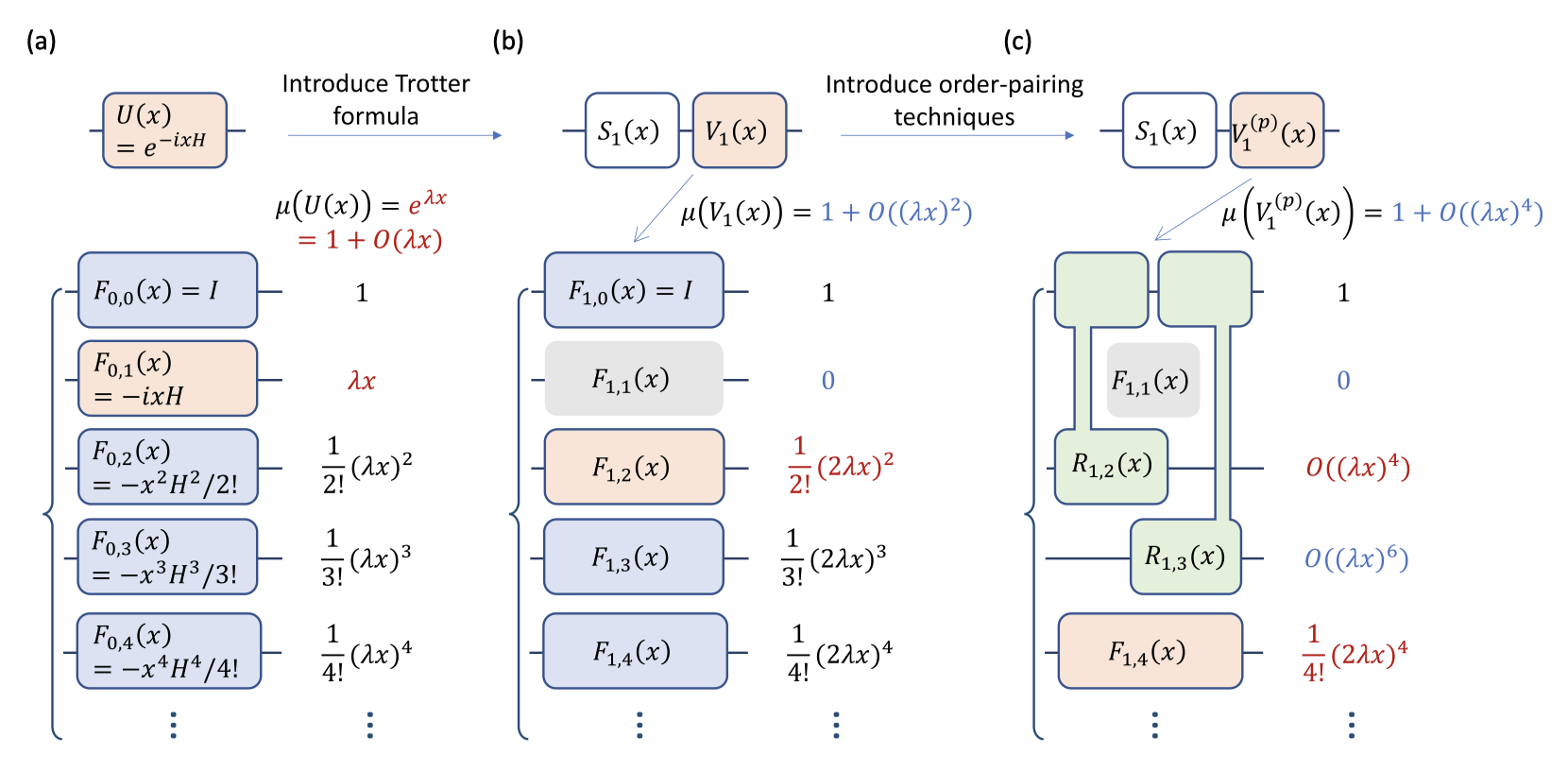
Trotter and linear combination of unitary (LCU) operations are two popular Hamiltonian simulation methods. The Trotter method is easy to implement and enjoys good system-size dependence endowed by commutator scaling, while the LCU method admits high-accuracy simulation with a smaller gate cost. We propose Hamiltonian simulation algorithms using LCU to compensate Trotter error, which enjoy both of their advantages. By adding few gates after the 𝐾th-order Trotter formula, we realize a better time scaling than 2𝐾th-order Trotter. Our first algorithm exponentially improves the accuracy scaling of the 𝐾th-order Trotter formula. For a generic Hamiltonian, the estimated gate counts of the first algorithm can be 2 orders of magnitude smaller than the best analytical bound of fourth-order Trotter formula. In the second algorithm, we consider the detailed structure of Hamiltonians and construct LCU for Trotter errors with commutator scaling. Consequently, for lattice Hamiltonians, the algorithm enjoys almost linear system-size dependence and quadratically improves the accuracy of the 𝐾th-order Trotter. For the lattice system, the second algorithm can achieve 3 to 4 orders of magnitude higher accuracy with the same gate costs as the optimal Trotter algorithm. These algorithms provide an easy-to-implement approach to achieve a low-cost and high-precision Hamiltonian simulation.
X. Yuan, J. Sun, J. Liu, Q. Zhao, and Y. Zhou, Phys. Rev. Lett., vol. 127, p. 040501, Jul 2021.
Tensor network theory and quantum simulation are, respectively, the key classical and quantum computing methods in understanding quantum many-body physics. Here, we introduce the framework of hybrid tensor networks with building blocks consisting of measurable quantum states and classically contractable tensors, inheriting both their distinct features in efficient representation of many-body wave functions. With the example of hybrid tree tensor networks, we demonstrate efficient quantum simulation using a quantum computer whose size is significantly smaller than the one of the target system. We numerically benchmark our method for finding the ground state of 1D and 2D spin systems of up to 8 ×8 and 9 ×8 qubits with operations only acting on 8 +1 and 9 +1 qubits, respectively. Our approach sheds light on simulation of large practical problems with intermediate-scale quantum computers, with potential applications in chemistry, quantum many-body physics, quantum field theory, and quantum gravity thought experiments.
Quantum Scientific Computing
Z.-X. Shang, N. Guo, D. An, and Q. Zhao, Phys. Rev. Lett., vol. 135, p. 120604, Sep 2025
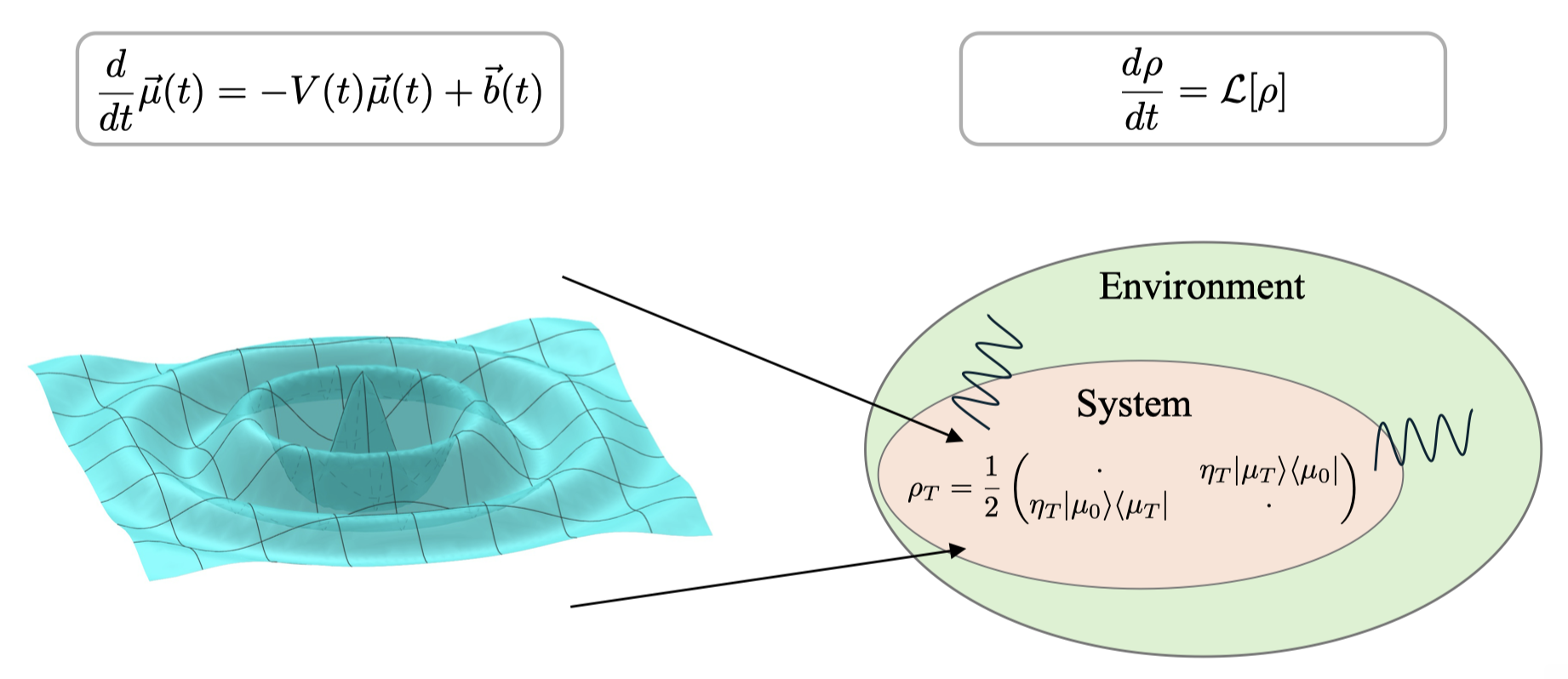
Solving linear ordinary differential equations (ODEs) is one of the most promising applications for quantum computers to demonstrate exponential advantages. The challenge of designing a quantum ODE algorithm is how to embed nonunitary dynamics into intrinsically unitary quantum circuits. In this Letter, we propose a new quantum algorithm for solving ODEs by harnessing open quantum systems. Specifically, we propose a novel technique called nondiagonal density matrix encoding, which leverages the inherent nonunitary dynamics of Lindbladians to encode general linear ODEs into the nondiagonal blocks of density matrices. This framework enables us to design quantum algorithms with both theoretical simplicity and high performance. Combined with the state-of-the-art quantum Lindbladian simulation algorithms, our algorithm can outperform all existing quantum ODE algorithms and achieve near-optimal dependence on all parameters under a plausible input model. We also give applications of our algorithm including the Gibbs state preparations and the partition function estimations.
D. An, J.-P. Liu, D. Wang, and Q. Zhao*, Communications in Mathematical Physics, vol. 406, no. 8, p. 189, 2025.
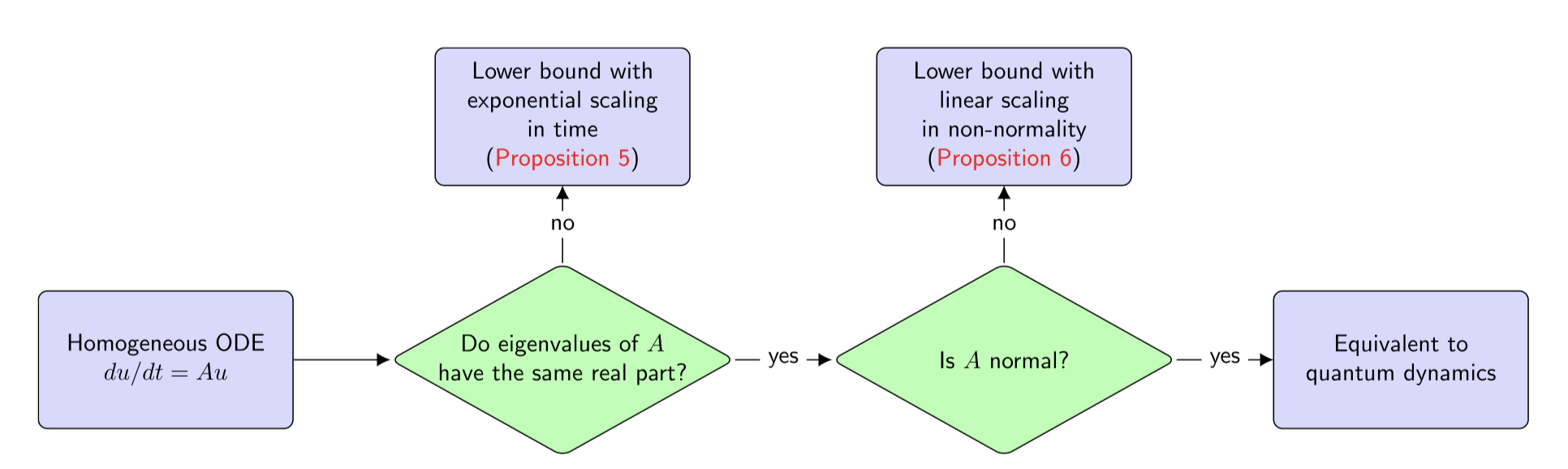
We study the limitations and fast-forwarding of quantum algorithms for linear ordinary differential equation (ODE) systems with a particular focus on non-quantum dynamics, where the coefficient matrix in the ODE is not anti-Hermitian or the ODE is inhomogeneous. On the one hand, for generic linear ODEs, by proving worst-case lower bounds, we show that quantum algorithms suffer from computational overheads due to two types of “non-quantumness”: real part gap and non-normality of the coefficient matrix. We then show that homogeneous ODEs in the absence of both types of “non-quantumness” are equivalent to quantum dynamics, and reach the conclusion that quantum algorithms for quantum dynamics work best. To obtain these lower bounds, we propose a general framework for proving lower bounds on quantum algorithms that are amplifiers, meaning that they amplify the difference between a pair of input quantum states. On the other hand, we show how to fast-forward quantum algorithms for solving special classes of ODEs which leads to improved efficiency. More specifically, we obtain exponential improvements in both T and the spectral norm of the coefficient matrix for inhomogeneous ODEs with efficiently implementable eigensystems, including various spatially discretized linear evolutionary partial differential equations. We give fast-forwarding algorithms that are conceptually different from existing ones in the sense that they neither require time discretization nor solving high-dimensional linear systems.
Quantum Information
Entanglement Detection
F. Shi, L. Chen, G. Chiribella, and Q. Zhao, Phys. Rev. Lett., vol. 134, p. 050201, Feb 2025.
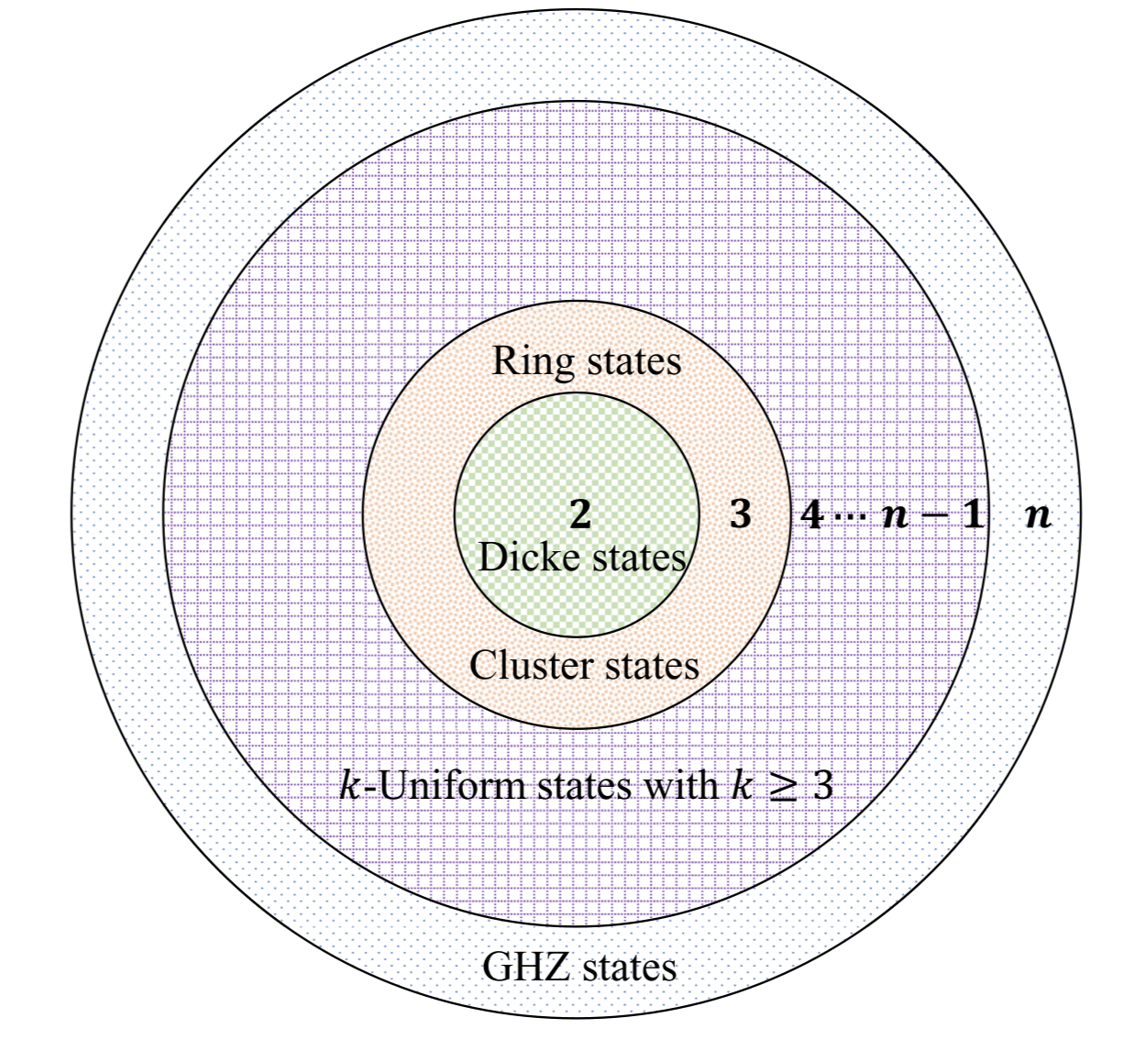
Multipartite entanglement is a valuable resource for quantum technologies. However, detecting this resource can be challenging: for genuine multipartite entanglement, the detection may require global measurements that are hard to implement experimentally. Here we introduce the concept of entanglement detection length, defined as the minimum number of particles that have to be jointly measured in order to detect genuine multipartite entanglement. For symmetric states, we show that the entanglement detection length can be determined by testing separability of the marginal states. For general states, we provide an upper bound on the entanglement detection length based on semidefinite programming. We show that the entanglement detection length is generally smaller than the minimum observable length needed to uniquely determine a multipartite state, and we provide examples achieving the maximum gap between these two quantities.
Z.-D. Li, Q. Zhao (Co-first author), R. Zhang, L.-Z. Liu, X.-F. Yin, X. Zhang, Y.-Y. Fei, K. Chen, N.-L. Liu, F. Xu, Y.-A. Chen, L. Li, and J.-W. Pan, Phys. Rev. Lett., vol. 124, p. 160503, Apr 2020.

Here, for the first time, we demonstrate MDIEW for multipartite entangled states. We experimentally detect the genuine entanglement and the entanglement structure of a tripartite entangled state based on an eight-photon interferometry. Furthermore, with the verified multipartite entangled state, we demonstrate quantum randomness generation and open-destination quantum key distribution in an measurement-device-independent manner.
H. Lu, Q. Zhao (Co-first author), Z.-D. Li, X.-F. Yin, X. Yuan, J.-C. Hung, L.-K. Chen, L. Li, N.-L. Liu, C.-Z. Peng, Y.-C. Liang, X. Ma, Y.-A. Chen, and J.-W. Pan, Phys. Rev. X, vol. 8, p. 021072, Jun 2018.
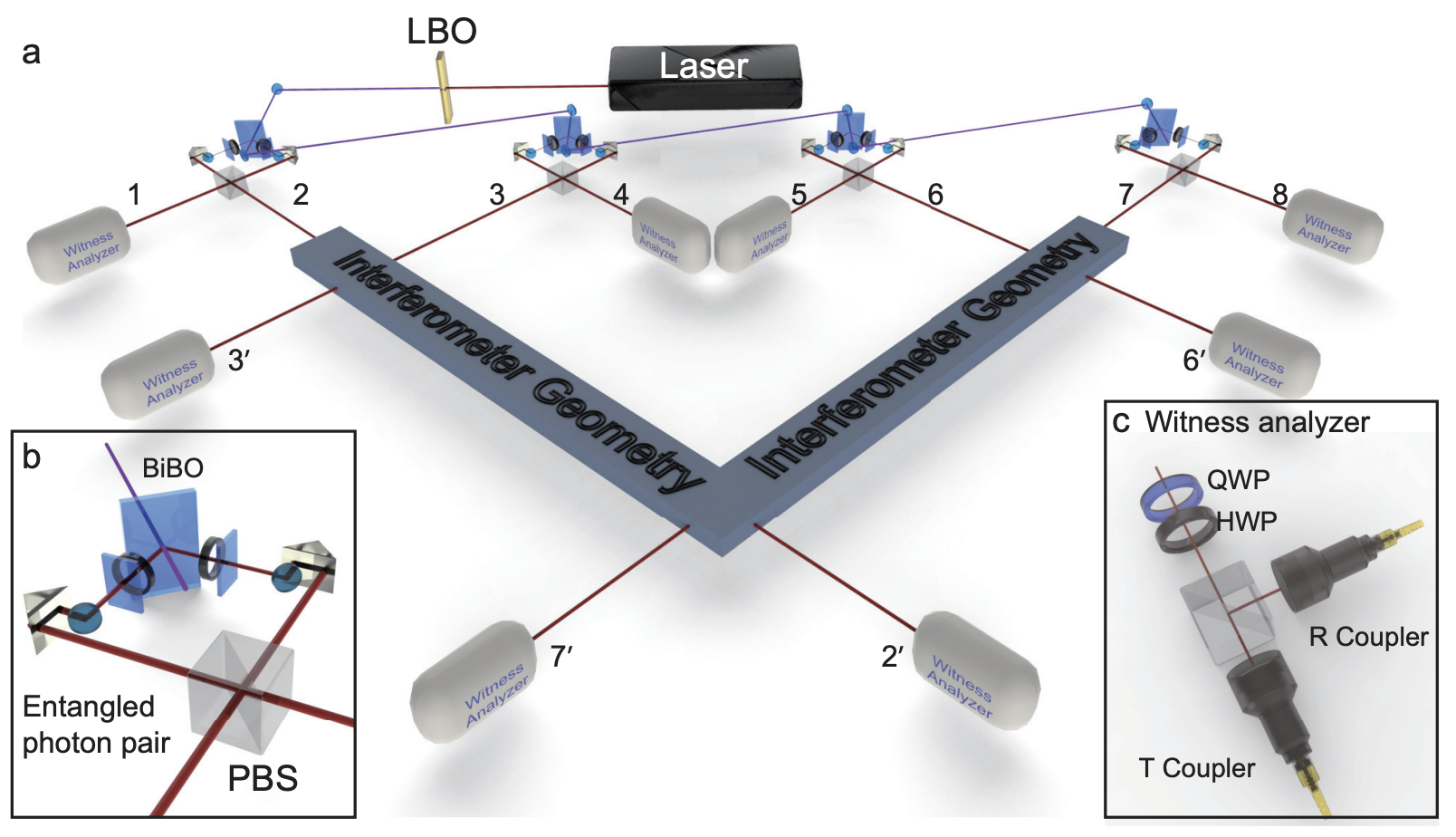
Here, we propose two complementary families of witnesses for the identification of such structures. They are based, respectively, on the detection of entanglement intactness and entanglement depth, each applicable to an arbitrary number of subsystems and whose evaluation requires only the implementation of solely two local measurements. Our method is also robust against noises and other imperfections, as reflected by our experimental implementation of these tools to verify the entanglement structure of five different eight-photon entangled states. In particular, we demonstrate how their entanglement structure can be precisely and systematically inferred from the experimental measurement of these witnesses. In achieving this goal, we also illustrate how the same set of data can be classically postprocessed to learn the most about the measured system.
Device-Independent
D. Wu, Q. Zhao (Co-first author), X.-M. Gu, H.-S. Zhong, Y. Zhou, L.-C. Peng, J. Qin, Y.-H. Luo,K. Chen, L. Li, N.-L. Liu, C.-Y. Lu, and J.-W., Phys. Rev. Lett., vol. 127, p. 230503, Dec. 2021
Here, we demonstrate the first robust self-testing for multi-particle quantum entanglement. We prepare two examples of four-photon graph states, the Greenberger-Horne-Zeilinger (GHZ) states with a fidelity of 0.957(2) and the linear cluster states with a fidelity of 0.945(2). Based on the observed input-output statistics, we certify the genuine four-photon entanglement and further estimate their qualities with respect to realistic noise in a device-independent manner.
Y. Liu, Q. Zhao, M.-H. Li, J.-Y. Guan, Y. Zhang, B. Bai,W. Zhang,W.-Z. Liu, C.Wu, X. Yuan, H. Li, W. J. Munro, Z.Wang, L. You, J. Zhang, X. Ma, J. Fan, Q. Zhang, and J.-W. Pan, Nature, vol. 562, no. 7728, p. 548, 2018.
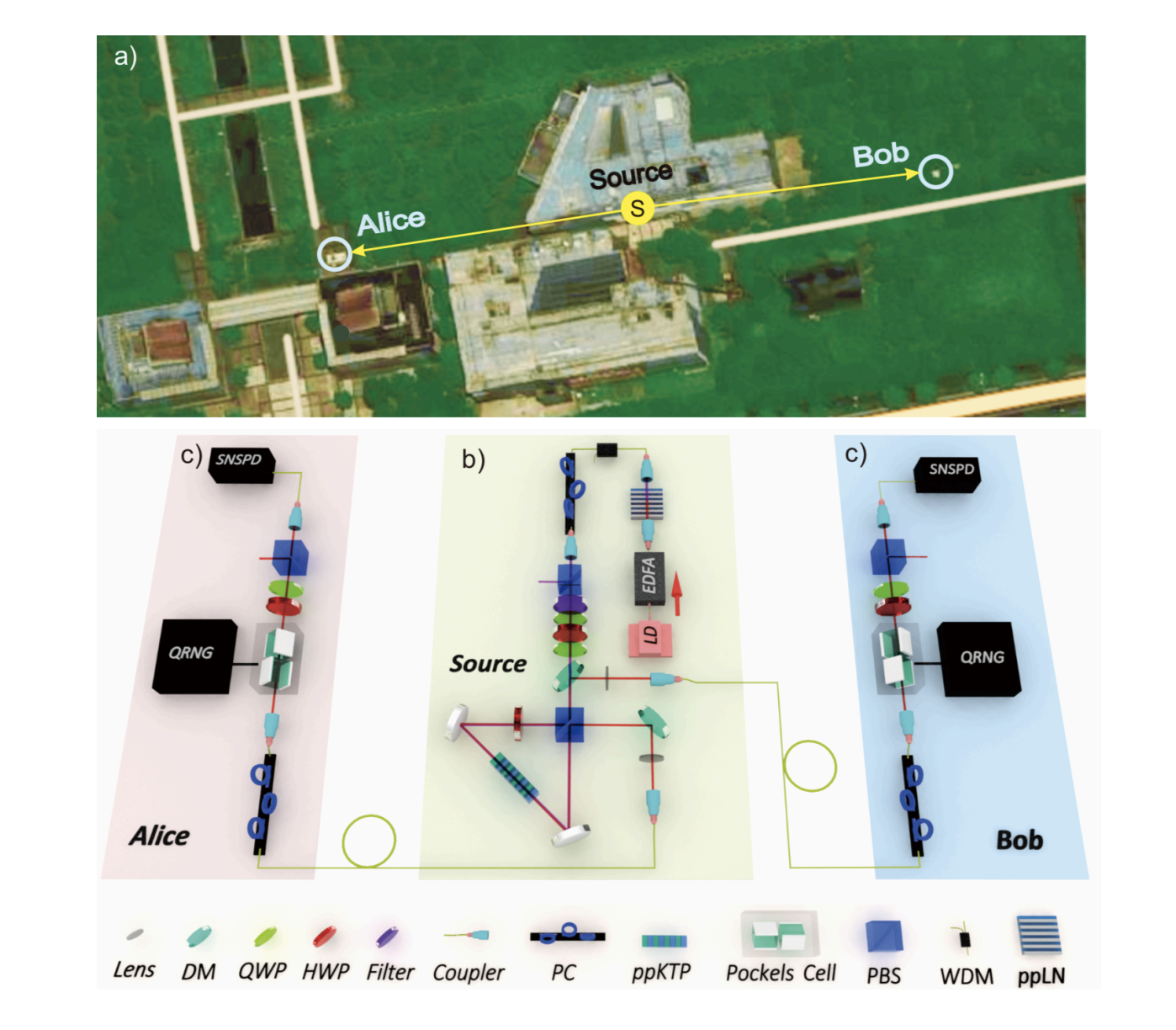
Here we present DIQRNG that is secure against quantum and classical adversaries10–12. We use state-of-the-art quantum optical technology to create, modulate and detect entangled photon pairs, achieving an efficiency of more than 78 per cent from creation to detection at a distance of about 200 metres that greatly exceeds the threshold for closing the ‘detection’ loophole of the Bell test.
H.-L. Huang, Q. Zhao, X. Ma, C. Liu, Z.-E. Su, X.-L.Wang, L. Li, N.-L. Liu, B. C. Sanders, C.-Y. Lu, and J.-W. Pan, Phys. Rev. Lett., vol. 119, p.050503, Aug 2017.
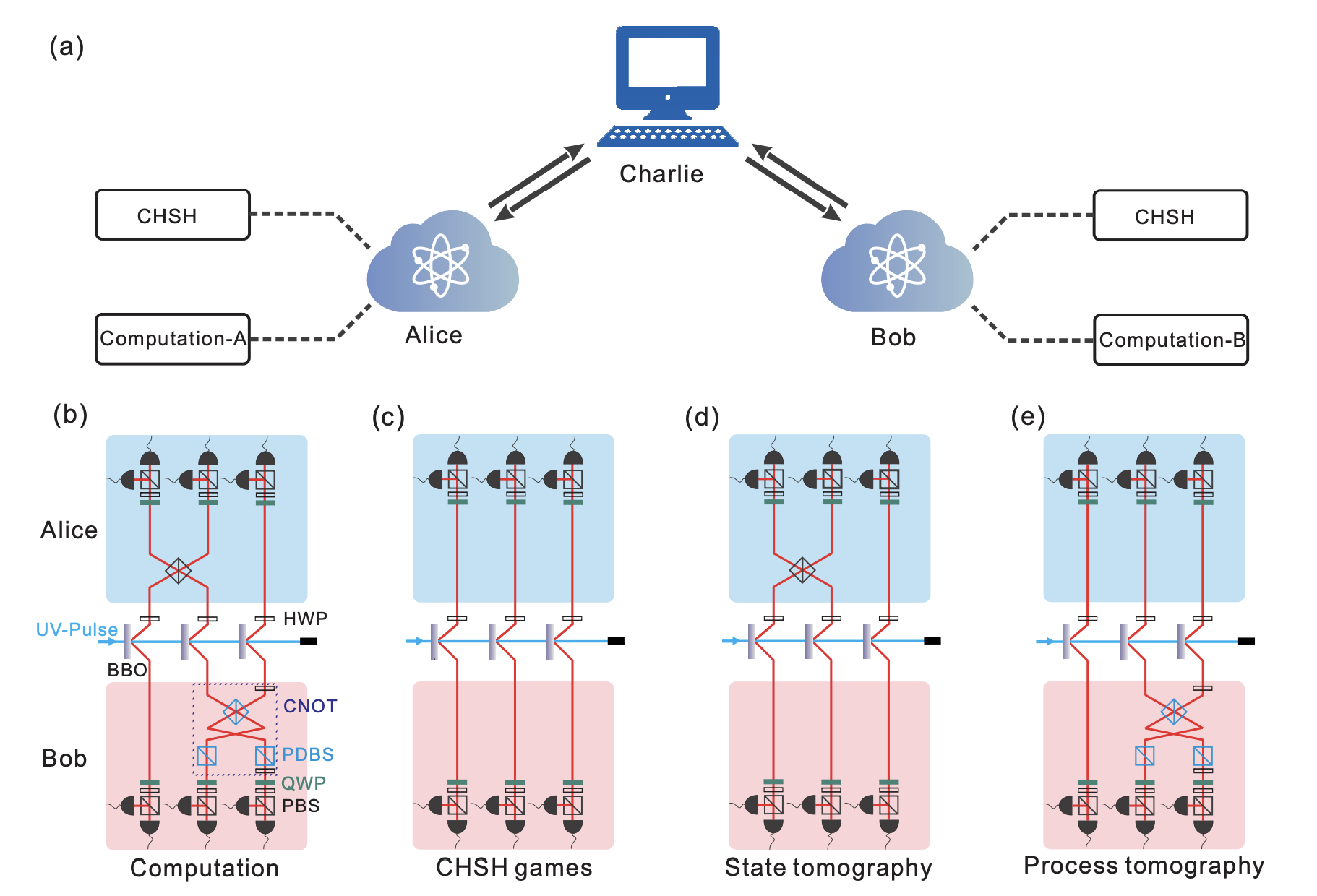
To date, blind quantum computing demonstrations require clients to have weak quantum devices. Here we implement a proof-of-principle experiment for completely classical clients. Via classically interacting with two quantum servers that share entanglement, the client accomplishes the task of having the number 15 factorized by servers who are denied information about the computation itself. This concealment is accompanied by a verification protocol that tests servers' honesty and correctness. Our demonstration shows the feasibility of completely classical clients and thus is a key milestone towards secure cloud quantum computing.